우주의 IT 소행성

n, m = map(int, input().split())
data = [] # 초기 맵
temp = [[0] * m for _ in range(n)] # 벽을 설치한 맵

for _ in range(n):
    data.append(list(map(int, input().split())))

dx = [-1, 0, 1, 0]
dy = [0, 1, 0, -1]
result = 0

def virus(x, y):
    for i in range(4):
        nx = x + dx[i]
        ny = y + dy[i]
        if nx >= 0 and nx < n and ny >= 0 and ny < m:
            if temp[nx][ny] == 0:
                temp[nx][ny] = 2
                virus(nx, ny)

def get_score():
    score = 0
    for i in range(n):
        for j in range(m):
            if temp[i][j] == 0:
                score += 1
    return score


def dfs(count):
    global result
    if count == 3:
        for i in range(n):
            for j in range(m):
                temp[i][j] = data[i][j]
        for i in range(n):
            for j in range(m):
                if temp[i][j] == 2:
                    virus(i, j)
        result = max(result, get_score())
        return

    for i in range(n):
        for j in range(m):
            if data[i][j] == 0:
                data[i][j] = 1
                count += 1
                dfs(count)
                data[i][j] = 0
                count -= 1

dfs(0)
print(result)

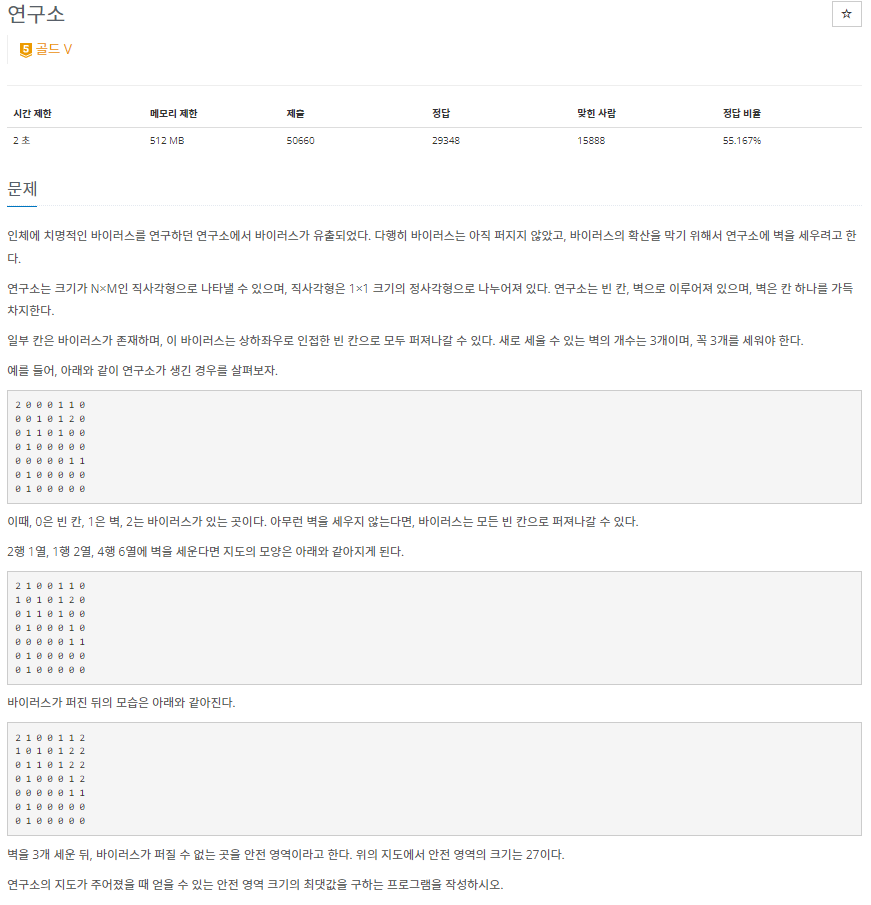
바이러스를 벽으로 어떻게 가두어야 제일 많은 안전 공간을 확보할 수 있냐의 문제이다.

주어진 벽은 총 3개, 맵의 크기는 8 * 8

총 64C3의 경우의 수를 모두 비교해 제일 많은 공간을 뽑아내면 된다.

비어있는 모든 공간에 3개의 벽을 설치하고, 그때마다의 안전 공간의 크기를 계산한 뒤 비교한다.

이렇게 연산하여 가장 많은 안전 공간을 출력해주면 된다.

BFS/DFS에 브루트포스가 함유된 알고리즘이었다.

DFS (Depth First Search, 깊이 우선 탐색)

- 그래프에서 깊은 부분을 우선 탐색하는 알고리즘

그래프란?

- 노드와 간선(정점)으로 표현된 자료구조

- 하나의 노드를 시작으로 다수의 노드를 방문하는 것을 그래프 탐색이라고 한다.

- 두 노드가 간선으로 이어져 있으면 '두 노드는 인접(Adjacent) 하다'라고 표현한다.

그래프의 표현 방식

- 그래프를 프로그래밍에서 표현하는 방식은 크게 2가지이다

1. 인접 행렬 방식 (Adjacency Matrix) : 2차원 배열로 그래프의 연결 관계를 표현

표로 표현했을 때

INF = 999999999 # 무한

# 2차원 리스트의 인접 행렬 표현
graph = [
	[0, 3, 5],
    [3, 0, INF],
    [5, INF, 0]
}

print(graph)

파이썬 코드로 표현했을 때

- 인접 행렬 방식은 모든 관계를 저장하므로 노드 개수가 많을수록 메모리의 낭비가 심함

- 인접 행렬 방식이 인접 리스트 방식보다 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 빠름

2. 인접 리스트 (Adjacency List) : 리스트로 그래프의 연결 관계를 표현

graph = [[] for _ in range(3)]

graph[0].append((1, 5))
graph[0].append((2, 3))

graph[1].append((0, 5))

graph[2].append((0, 3))

print(graph)

- 인접 리스트 방식은 연결된 정보만을 저장하기 때문에 메모리를 효율적으로 사용함

- 인접 리스트 방식은 두 노드가 연결되어 있는지에 대한 정보를 얻는 속도가 느림 (데이터를 하나씩 확인)

# DFS
def dfs(graph, v, visited):
	visited[v] = True
    print(v, end=' ')
    for i in graph[v]:
    	if not visited[i]:
        	dfs(graph, i, visited)

graph = [
	[],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

visited = [False] * 9
dfs(graph, 1, visited)

BFS (Breadth First Search, 너비 우선 탐색)

- 가까운 노드부터 탐색하는 알고리즘

- DFS와 반대(가장 가까운 노드부터 / 가장 먼 노드부터)

- 선입선출의 큐 자료구조를 사용

- 재귀로 DFS를 구현하면 수행 시간이 느려질 수 있음

- 스택을 사용하여 DFS구현을 빠르게 동작시킬 수 있음

- 일반적인 경우 DFS보다 BFS의 동작이 빠름

# BFS
from collections import deque

def bfs(graph, start, visited):
	queue = deque([start])
    visited[start] = True
    while queue:
    	v = queue.popleft()
        print(v, end=' ')
        for i in graph[v]:
        	if not visited[i]:
            	queue.append(i)
                visited[i] = True

graph = [
	[],
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

visited = [False] * 9
bfs(graph, 1, visited)

탐색(Search)

- 다수의 데이터 속 원하는 데이터를 찾는 과정

- 그래프 트리 등의 자료구조 안에서 사용하는 대표적인 탐색 알고리즘으로 BFS/DFS가 있다.

- BFS/DFS 탐색를 이해하려면 기본 자료구조에 대한 사전 지식이 수반되어야 한다.

자료구조(Data Structure)

- 데이터를 표현/관리/처리 하기 위한 구조

- 스택 / 큐 / 덱 / 그래프 / 트리 등이 있다

오버플로(Overflow)

- 특정 자료구조의 수용 범위를 넘어섰을 때, 추가로 데이터를 삽입할 때 나타나는 연산 오류

- Over(넘쳐) + flow(흐르다) ->> 데이터가 너무 많아서 넘쳐 흘러 버린다.

언더플로(Underflow)

- 오버플로의 반대로, 데이터가 전혀 없는데 데이터를 삭제할 때 나타나는 연산 오류

스택(Stack)

- 박스 쌓기와 같은 구조

- 박스는 아래서부터 위로 차곡차곡 쌓고, 아래의 박스를 꺼내려면 위의 박스를 치워야만 한다.

- 선입후출(First in Last Out / FILO) -> 먼저 들어온게(선입), 나중에 나간다(후출)

- 파이썬 리스트의 append()와 pop() 함수를 사용하면 stack과 동일하게 사용할 수 있다.

큐(Queue)

- 마트의 대기 줄이나 도로의 터널을 생각해보자.

- 먼저 들어온 (대기한) 사람이 먼저 나가는(우선권을 가지는) 자료구조로 선입선출(First In First Out / FIFO)이다.

- 파이썬 collections 모듈의 deque 자료 구조를 사용하자 (스택과 큐의 장점 둘 다를 가짐)

재귀 함수(Recursive Function)

- 자기 자신을 다시 호출하는 함수

# 예시
def recursive_function():
	print("나 불렀어?")
    recursive_function()

recursive_function()

이 경우에는 "나 불렀어?"가 무한히 출력된다.

파이썬에서는 재귀함수의 무한 출력을 방지하기 위해 횟수 제한을 두고있다. (기본 1000회)

따라서 코드 시작에

import sys
sys.setrecursionlimit(횟수)

를 삽입하여 필요에 따라 재귀함수의 출력 최대 횟수를 지정해주자.

하지만 애초에 재귀 함수를 사용할 때는 무한 출력이 발생하지 않도록, 종료 조건을 명시해주어야 한다.

컴퓨터 내부에서 재귀함수는 스택 자료구조를 이용한다.

따라서 가장 마지막에 호출된 재귀함수가 끝나야 순차적으로 앞선 호출이 완료되는 것이다.