우주의 IT 소행성

https://www.acmicpc.net/problem/16197

n, m = map(int, input().split())
a = [list(input()) for _ in range(n)]
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
location = []

for i in range(n):
    for j in range(m):
        if a[i][j] == 'o':
            location.append((i, j))

x1, y1 = location[0]
x2, y2 = location[1]


def go(x1, y1, x2, y2, count):
    is_fall = [False, False] # 동전이 떨어졌는지 여부 파악

    # 버튼을 10번 넘게 누른 경우
    if count == 11:
        return -1

    if (x1 < 0 or x1 >= n or y1 < 0 or y1 >= m):
        is_fall[0] = True
    if (x2 < 0 or x2 >= n or y2 < 0 or y2 >= m):
        is_fall[1] = True

    if is_fall[0] and is_fall[1]:  # 둘 다 떨어진 경우 (불가능)
        return -1

    if is_fall[0] or is_fall[1]:  # 하나만 떨어진 경우 (정답)
        return count

    ans = -1
    for i in range(4):
        nx1, ny1 = x1 + dx[i], y1 + dy[i]
        nx2, ny2 = x2 + dx[i], y2 + dy[i]

        # 이동할 칸이 벽이라면 이동하지 않는걸로
        if 0 <= nx1 < n and 0 <= ny1 < m and a[nx1][ny1] == '#':
            nx1, ny1 = x1, y1
        if 0 <= nx2 < n and 0 <= ny2 < m and a[nx2][ny2] == '#':
            nx2, ny2 = x2, y2

        # 다음 칸으로 진행시켰는데
        temp = go(nx1, ny1, nx2, ny2, count + 1)
        if temp == -1:  # -1 받았다면 무시
            continue
        if ans == -1 or ans > temp:  # -1이 아니라면(정답이라면)
            ans = temp
    return ans

print(go(x1, y1, x2, y2, 0))

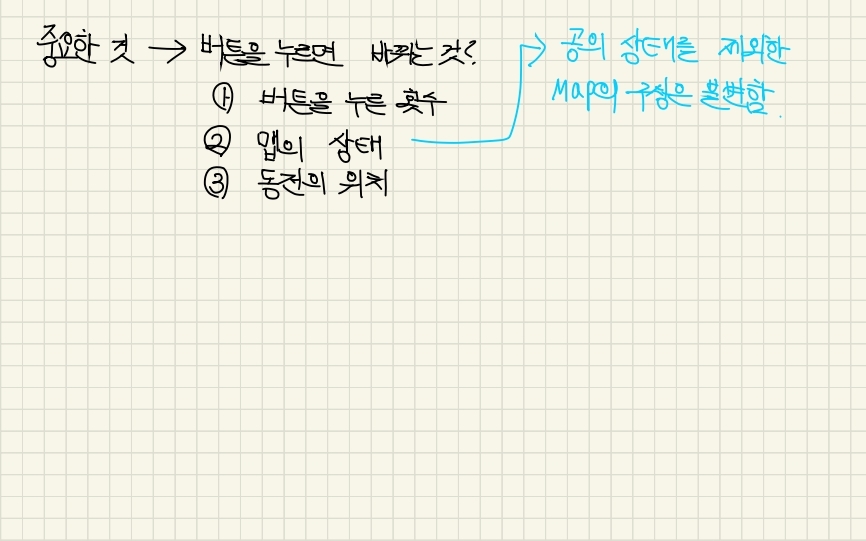
네 개의 버튼 (상하좌우)를 통해 두 동전을 동시에 이동시키는데

1. 동전이 벽에 가로 막히면 제자리

2. 동전 하나가 떨어지면 정답

3. 동전 2개가 동시에 떨어지는건 불가능

4. 버튼을 10번이상 사용하면 무효

라는 4가지 조건을 지키며 재귀함수를 통해서 풀어주었다

https://noj.am/11054 

n = int(input())
a = list(map(int, input().split()))
d = [0] * n
d2 = [0] * n

# 가장 긴 증가하는 부분 수열 찾기
for i in range(n):
    d[i] = 1 # 만약 증가하지 않는다면 1로 초기화
    for j in range(i):
        if a[i] > a[j] and d[i] < d[j] + 1:
            d[i] = d[j] + 1

# 가장 긴 감소하는 부분 수열 찾기
for i in range(n - 1, -1, -1):
    d2[i] = 1
    for j in range(i + 1, n):
        if a[i] > a[j] and d2[i] < d2[j] + 1:
            d2[i] = d2[j] + 1

result = [d[i] + d2[i] - 1 for i in range(n)]
print(max(result))

바이토닉 수열
증가하다가 어떤 기점을 중심으로 다시 감소하는 수열.
즉 i번째에서 끝나는 가장 긴 증가하는 부분수열 + i번째에서 시작하는 가장 긴 감소하는 부분수열이다.

https://www.acmicpc.net/problem/1309

n = int(input())
d = [[0] * 3 for _ in range(n + 1)]
d[0][0] = 1

for i in range(1, n + 1):
    d[i][0] = d[i - 1][0] + d[i - 1][1] + d[i - 1][2]
    d[i][1] = d[i - 1][0] + d[i - 1][2]
    d[i][2] = d[i - 1][0] + d[i - 1][1]
    for j in range(3):
        d[i][j] %= 9901
print(sum(d[n]) % 9901)

D[N] = 세로로 n칸인 동물원에서 가능한 배치의 수
d[n][m] = 세로로 n칸인 동물원, 마지막 칸은 m번 방법을 사용한 배치의 수
m : 0 배치하지 않음
m : 1 왼쪽 배치
m : 2 오른쪽 배치

https://www.acmicpc.net/problem/1149

n = int(input())
a = [[0, 0, 0]] + [list(map(int, input().split())) for _ in range(n)]
d = [[0, 0, 0] for _ in range(n + 1)]

for i in range(1, n + 1):
    d[i][0] = min(d[i - 1][1], d[i - 1][2]) + a[i][0]
    d[i][1] = min(d[i - 1][0], d[i - 1][2]) + a[i][1]
    d[i][2] = min(d[i - 1][0], d[i - 1][1]) + a[i][2]
print(min(d[n][0], d[n][1], d[n][2]))

RGB 거리, R = 0, G = 1, B = 2 라고 하고
A[i][j] = i번 집이 j번색일 경우 로 가정하자.
1. i의 이웃은 i - 1, i + 1
2. 첫 집과 마지막 집은 이웃이 아니다.
3. 모든 이웃은 다른 색의 집이다.
- 연속하는 집을 같은 색으로 칠할 수 없다.

d[i][0] = min(d[i - 1][1], d[i-1][2]) + a[i][0]
d[i][1] = min(d[i - 1][0], d[i-1][2]) + a[i][1]
d[i][2] = min(d[i - 1][0], d[i-1][1]) + a[i][2]
정답 : min(d[n][0], d[n][1], d[n][2])